[新しいコレクション] parabola (y-k)^2=4p(x-h) 163014-What is 4p in parabola

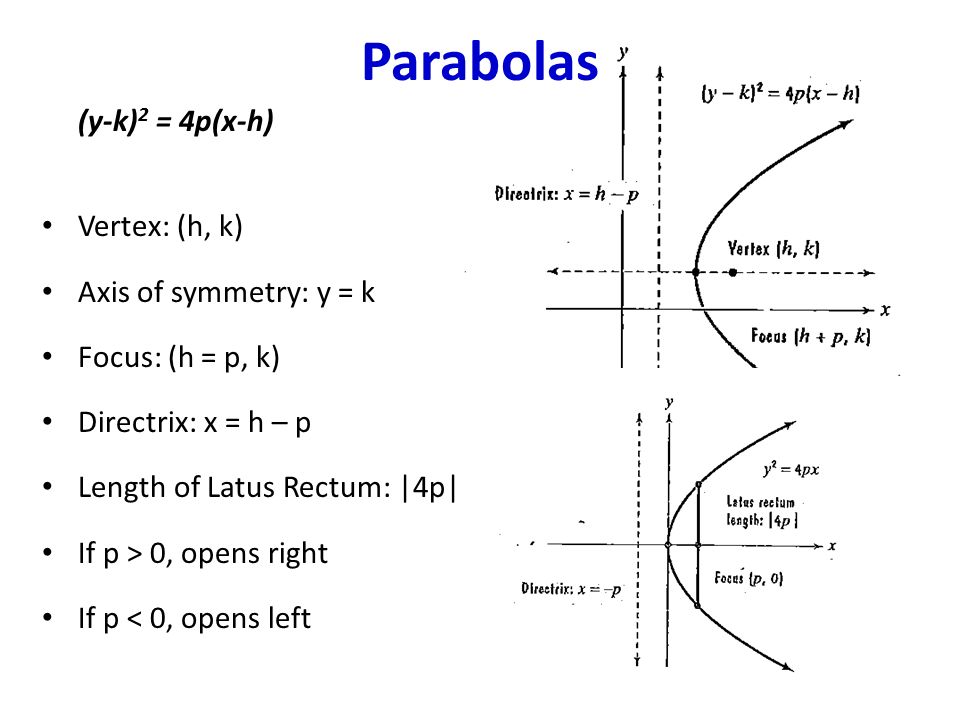
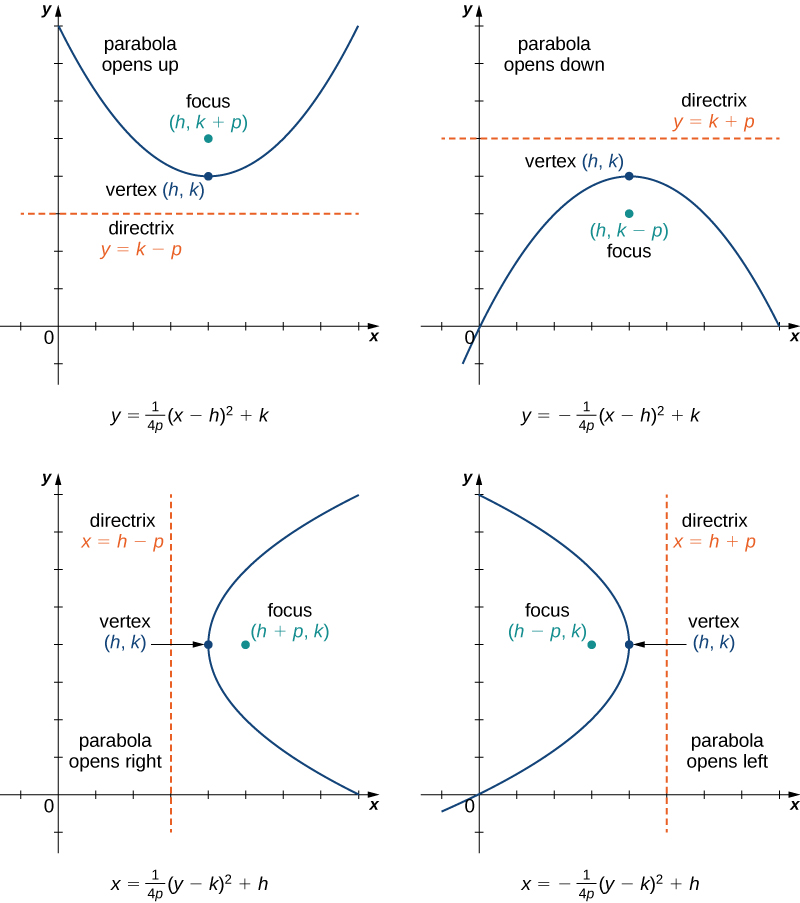
Its graph is shown Thereof, how do you tell if a parabola is vertical or horizontal?The standard form is (x h)2= 4p (y k), where the focusis (h, k p) and the directrix is y = k p If the parabola is rotatedso that its vertex is (h,k) and its axis of symmetry is parallel to thexaxis, it has an equation of (y k)2= 4p (x h), where thefocus is (h p, k) and the directrix is x = h pAnd directrix, write down its equation in the form (xh)2 = 4p(yk) or (yk)2 = 4p(xh) • Graph a parabola given in the form (x h)2 = 4p(y k) or (y k)2 = 4p(x h) and locate its focus, directrix, and axis of symmetry • Givenanequationofaparabolainageneralformlike4x x8y57 = 0,rewrite it in a standard form (xh)2 = 4p(yk) or (yk)2 = 4p(xh) 225

Parabola Definition And Equation

What is 4p in parabola

What is 4p in parabola- The vertex is (2,3) The focus is (5,3) The diretrix is x=1 Let's put y on one side of the equation and x on the other y^26y=12x33 We complete the square for the left side of the equation y^26y99=12x33 (y3)^29=12x33 (y3)^2=12x24 (y3)^2=12(x2) Since this is in the form of (yk)^2=4p(xh), we know this is a horizontal parabola Now, we can figure out that h=2, k Step 1 use the (known) coordinates of the vertex, (h,k), to write the parabola's equation in the form y=a (x−h)2k Step 2 find the value of the coefficient a by substituting the coordinates of point P into the equation written in step 1 and solving for a

Solved A Write The Equation Of The Parabola In Standard Form X H 2 4p Y K And Find The Vertex By Completing The Square 3x2 6x 6y 9 B Graph And Label The Center And Four Points X 1 2 Over 9 Y 1 2

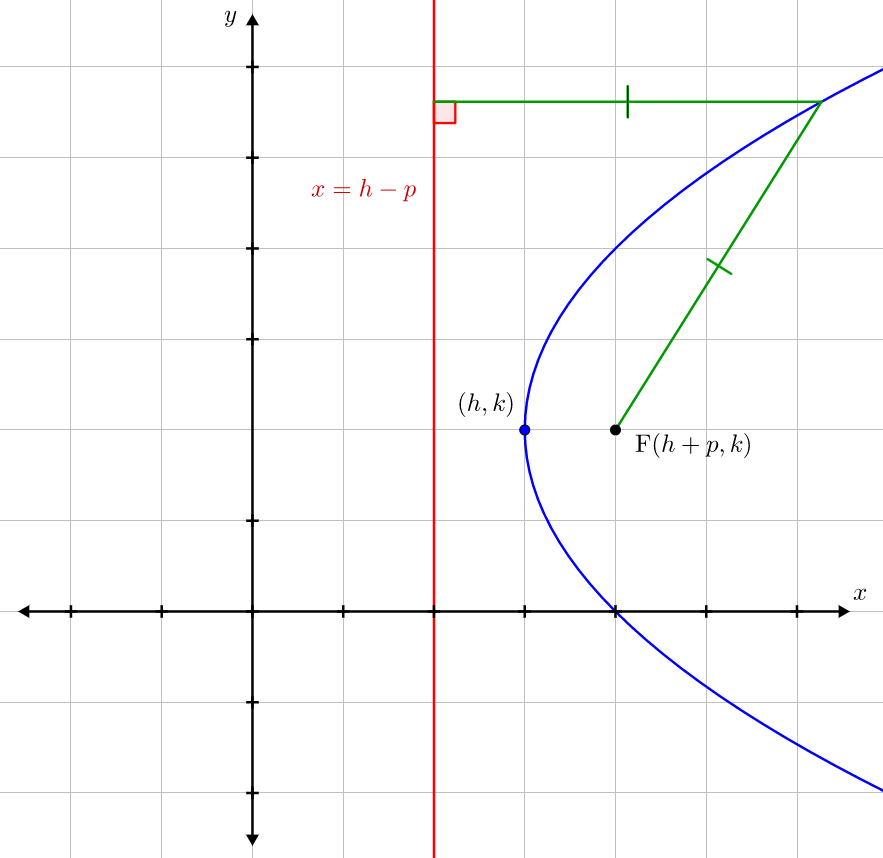
Answer (1 of 2) Midpoint of latus rectum is focus of parabola F = (2,1) Length of latus rectum = (5(3)) 8 units 4p = 8, p = 2 Focus is in first quadrant and Latus rectum is segment on line X = 2, so parabola is horizontal and opens towards right So vertex of this parabola is (f(x)p,k) `y^2=28x` Take note that one of the vertex form of parabola is `(y k)^2 = 4p(xh)` where (h,k) is the vertex and, p is the distance between vertex and focus and also the same distance between2 PARABOLA with vertex at (0,0) y2 4px Opens left or right x2 4py Opens up or down 3 PARABOLA (y k) 2 4p (x h) Opens left or right

Directrix is y = k pThe equation 4a(xh)=(yk) 2 generates a parabola which opens to the right if a>0 and opens to the left if aChoose from 63 different sets of termparabolas = (x h)^2=4p(y k) (y k)^2=4p(x h) flashcards on Quizlet Log in Sign up termparabolas = (x h)^2=4p(y k) (y k)^2=4p(x h)

If we take the equation (x − h) 2 =4p(y − k) and expand it we get x 2 − 2hx h 2 = 4py − 4pk or x 2 − 2hx − 4py 4pk h 2 = 0 which is an equation of the form x 2 Ax By C=0, where A, B and C are constants We ask if we are given such an equation can we recognize it as the equation of a parabola? with vertex ( h, k ) and the horizontal line y = k as its axis of symmetry If a > 0, then the parabola opens to the right, otherwise if a < 0, then the parabola opens to the left Observe than when the vertex ( h, k ) = ( 0, 0 ) and either a = 1 or a = – 1, the graphs of the vertical and horizontal parabolas are mirror images of each other with respect to the vertical axis ofImage transcriptions The equation of directrix is 4 = 4 50 , the axis of the parabola is parallel to y axis Hence, the equation of the parabola is of the form ( x K ) " = 4p (y h ) Where the coordinates of the focus are ( K , h p) and the equation of the directrix is y = hp The given coordinates of the focus are (5 , 6 ) and the equation of directrix is y = 4 So, we get the

Solved Left Right Y K 2 4p X H Directions Use What You Chegg Com

Graphing Parabolas With Vertices Not At The Origin College Algebra

If the focus is below the directrix, then the parabola opens down and {eq}pAnyway, it's because the equation is actually in the conic form for a parabola That's the form 4p(y – k) = (x – h)2 We recognize h and k from the vertex form of a parabola as, well, the vertex, (h, k) They've kept that job, despite the company restructuringStart studying Parabola (xh)^2=4p(yk) Learn vocabulary, terms, and more with flashcards, games, and other study tools

Find The Equation Of A Parabola Given Three Points In X H 2 4p Y K Mathematics Stack Exchange

Hpc Cu 10 11 8 1 Parabolas By Math Hammy Teachers Pay Teachers

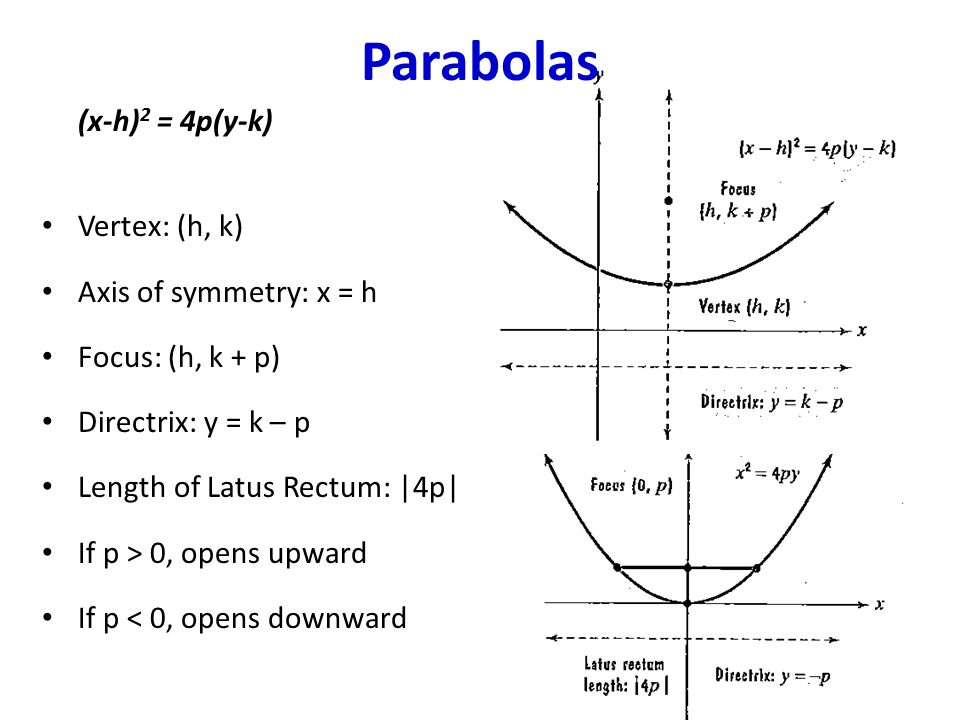
±p distance away from the vertex;Given parabola opens upward Basic form of equation (xh)^2=4p (yk) vertex (0,1) (midway between focus and directrix on the axis of symmetry) axis of symmetry y=0 or xaxis p=4 (distance from vertex to focus or directrix on the axis of symmetry 4p=16 equation (x)^2=16 (yk)Coming to the equation of parabola, If a parabola has a vertical axis, the standard form of the equation of the parabola is (x – h) 2 = 4p(y – k), where p≠ 0 The vertex of this parabola is at (h, k)The focus is at (h, k p)The directrix is the line y = k – pThe axis is the line x = h f a parabola has a horizontal axis, the standard form of the equation of the parabola is this

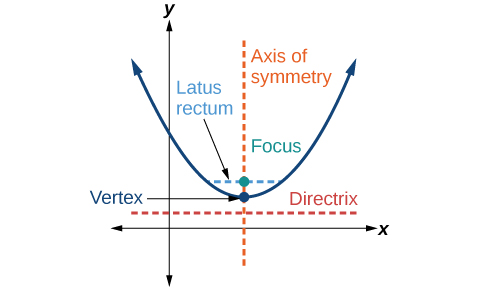
8 4 The Parabola Mathematics Libretexts

Math Test Conic Sections Flashcards Quizlet

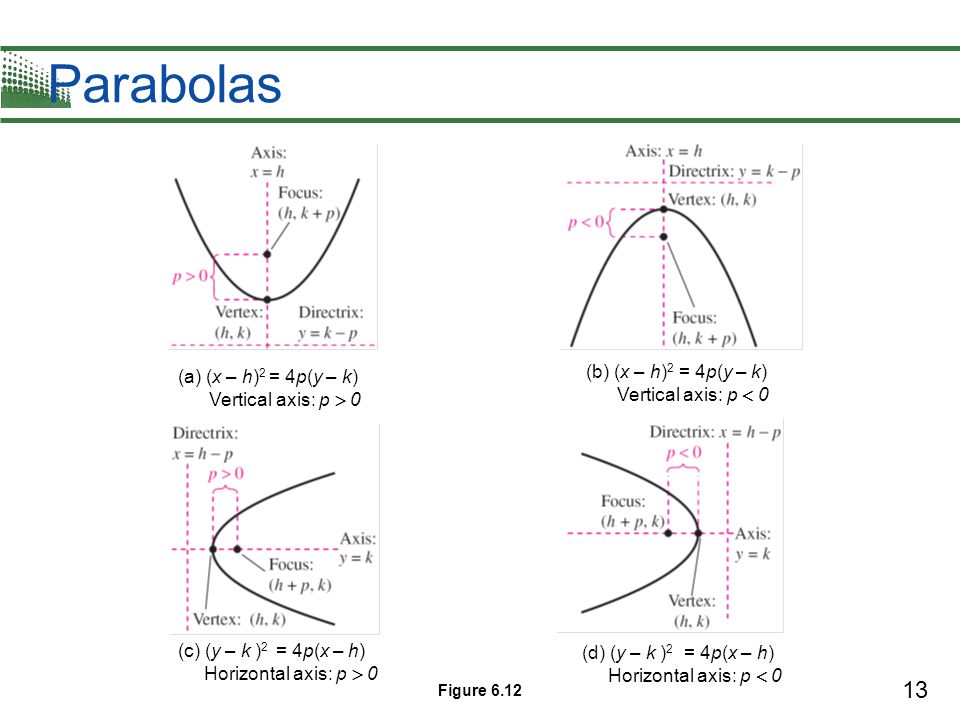
The squaring of the variables in the equation of the parabola determines where it opens When the x is squared and y is not, the axis of symmetry is vertical and the parabola opens up or down For instance, y = x 2 is a vertical parabola; Note • (x h)2 = 4p (y k) Parabola open up (U) if p>0 and opend down (D) if p0 and opend to the left (L) if p 4p(y – k) = (x – h)2 (x­h)2=4p(y­k) (y­k)2=4p(x­h) or or (y­k) = 1/4p (x­h)2 (x­h) = 1/4p (y­k)2 y=ax2 y=(1/4p)x2 a = 1/4p "Conics" equation of a parabola with Horizontal directrix Vertical Directrix Apr 23­300 PM If the vertex of the parabola is at (h,k) and the distance between the vertex and the focus is p, then the following 4

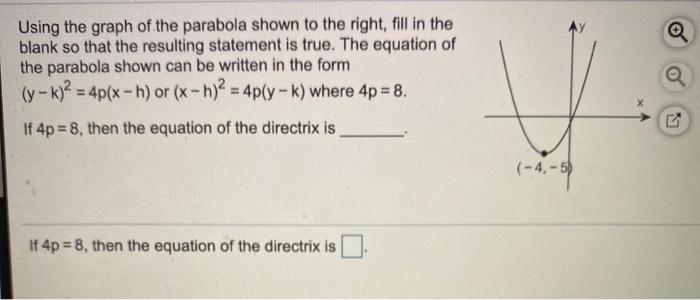
Solved Using The Graph Of The Parabola Shown To The Right Chegg Com

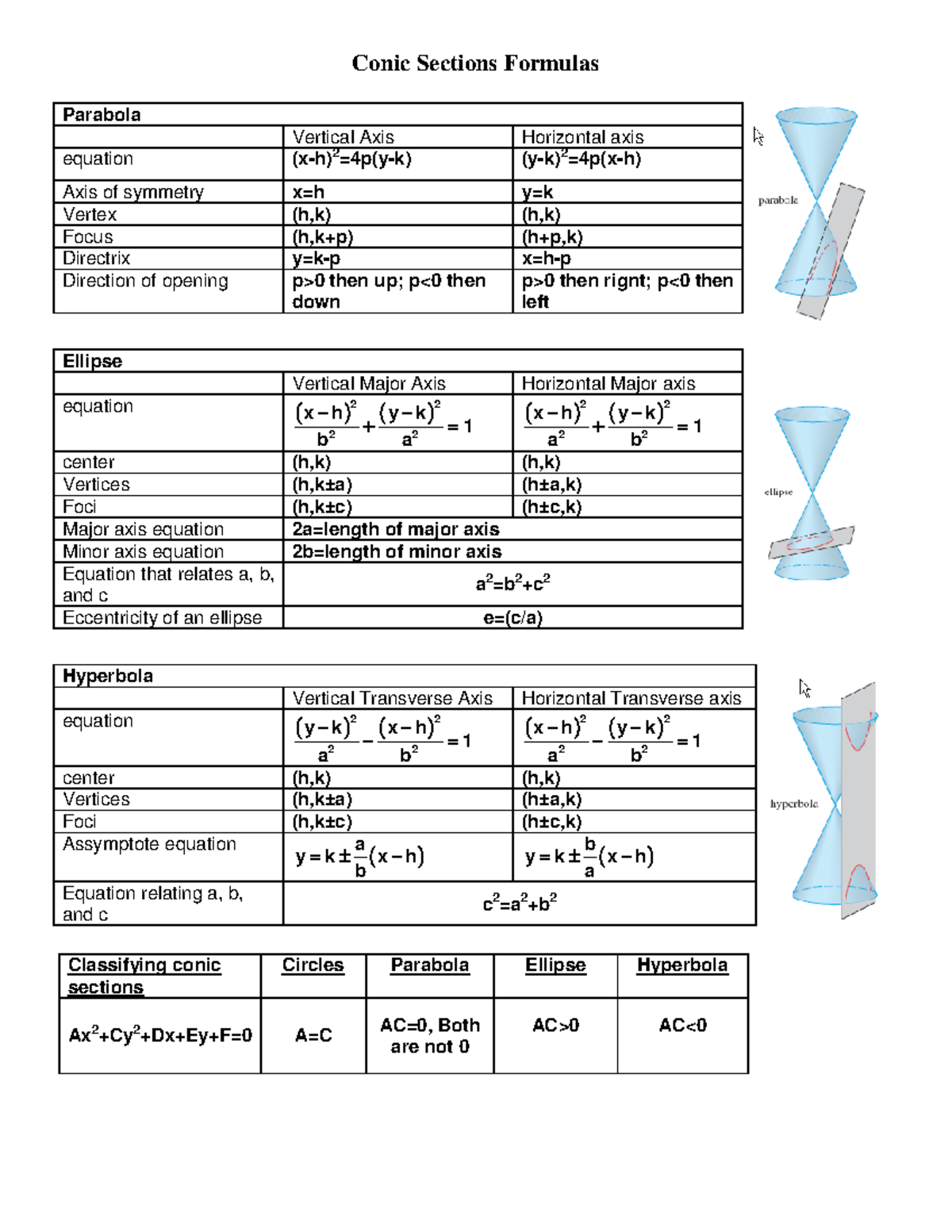
Conic Sections Formulas Essay Introduction Conic Sections Formulas Parabola Vertical Axis Studocu

 An equation for the parabola would be y²=19x (yk)²=4p(xh), where (h, k) is the vertex, (hp, k) is the focus and x=hp is the directrix Which is the equation of a parabola with vertex 0 0 and Directrix x = 2?, Answer Expert Verified The directrix line located at x=2 which makes a vertical line(y k) 2 = 4p(x h) x = a(y k) 2 h note a = 4p 3 where is the focus of a parabola located? y = ɑ(x h) 2 k Using Pythagoras's Theorem we can prove that the coefficient ɑ = 1/4p, where p is the distance from the focus to the vertex When the axis of symmetry is parallel to y axis Substituting for ɑ = 1/4p gives us y = ɑ(x h) 2 k = 1/(4p)(x h) 2 k Multiply both sides of the equation by 4p 4py = (x h) 2 4pk

Parabola Conic Section Warmup Graph The Following Parabola

Lesson 4 Parabolas In This Lesson Students Will Become Familiar With The Equations And Graphs Of Parabolas The Definition Of A Parabola Will Be Learned Both Algebraically And Using The Distance Relationship Students Will Learn How To Construct A Parabola

If the x is squaredGiven an equation of a parabola (x − h)2 = 4p (y− k) or (y − k)2 = 4p (x − h), how can you determine whether the parabola opens vertically or horizontally? The vertex is at (h, k) What is 4p parabola?

More Conic Sections Objective Given A Translation I Can Graph An Equation For A Conic Section Ppt Download

Pslv Conic Section

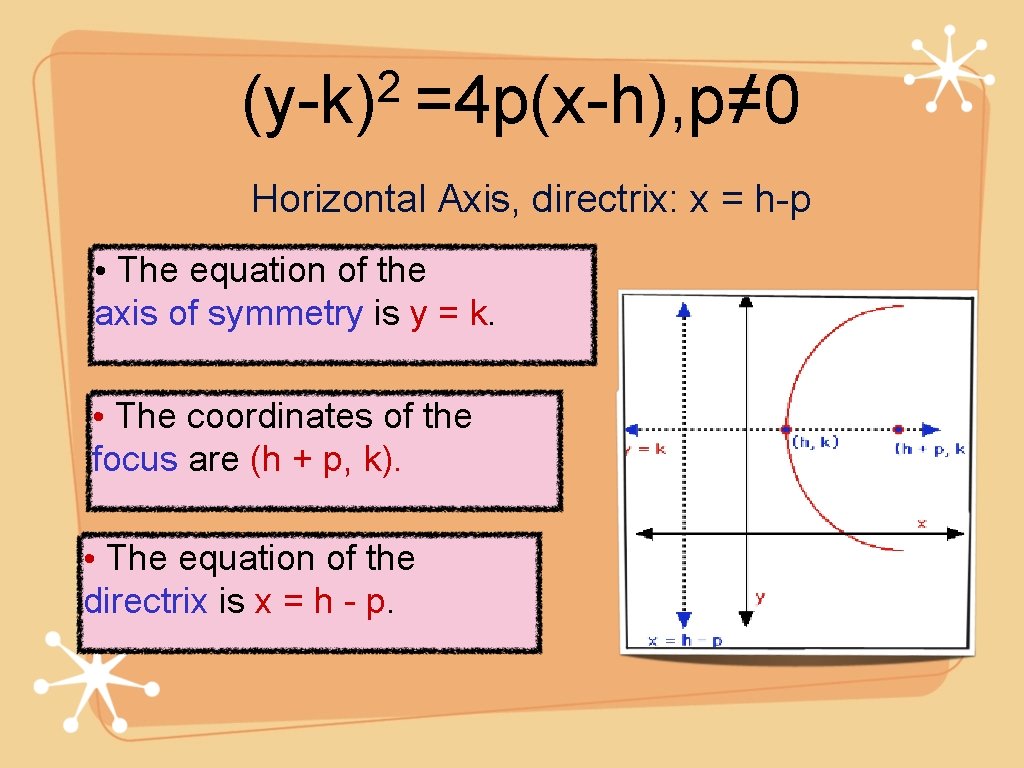
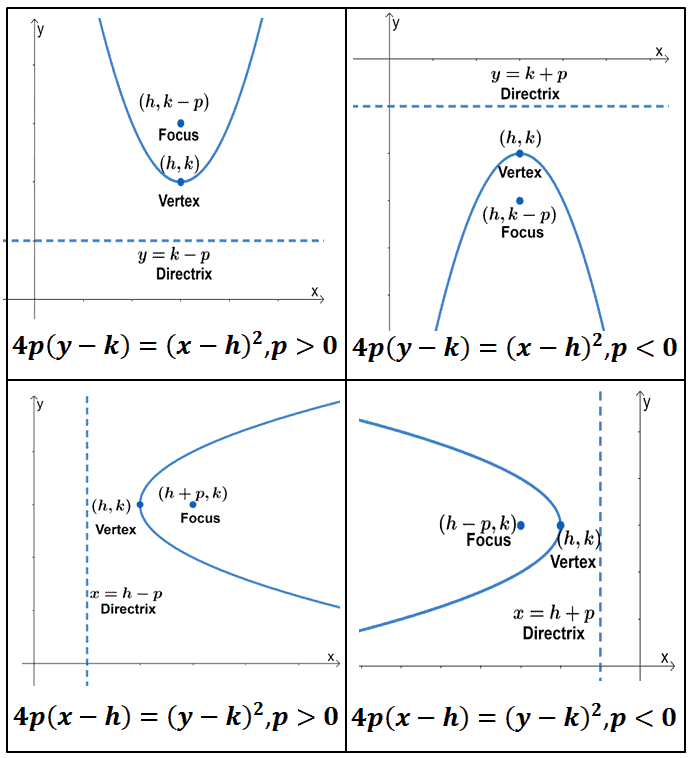
For this kind of parabola, the attention is centered at the point (h, k p) and the directrix is a lineup located at y = k p On the flip side, the equation of a parabola calculator with a vertex at (h, k) and a horizontal axis of symmetry is described as (y k)^2 = 4p(x h)The standard form for the equation of a parabola is x2 = 4yp (opens up) or y2 = 4xp (opens to right) The transformed form which moves the vertex from the origin to (h;k) is y k = 4p(x h) 2 or x h = 4p(y k) 2To graph parabolas with a vertex (h,k) ( h, k) other than the origin, we use the standard form (y−k)2 =4p(x−h) ( y − k) 2 = 4 p ( x − h) for parabolas that have an axis of symmetry parallel to the x axis, and (x−h)2 = 4p(y−k) ( x − h) 2 = 4 p ( y − k) for parabolas that have an axis of symmetry parallel to the y

Precalculus Algebra Review Conic Sections 10 Of 27 The Parabola Standard Form Ex 4 Youtube

Focus Of A Parabola

Learn how to graph a parabola in the form y=(xh)^2k!Make sure to like this video if you found it helpful and feel free to leave feedback in the comments seIf p > 0, the parabola opens upward, and if p < 0, the parabola opens downward If a parabola has a horizontal axis, the standard form of the equation of the parabola is this (y k)2 = 4p(x h), where p≠ 0 The vertex of this parabola is at (h, k) The focus is at (h p, k) The directrix is the line xTitle Parabolas 1 Section 102 Parabolas;

Parabola Definition And Equation

Solution Find An Equation In Standard Form Of The Parabola Described Vertex At 4 2 Passes Through 3 0 And 9 4 3 Standard Form Y K 2 4p X H

 Here the equation is horizontal parabola standard form (y k) 2 = 4p(x h) If given the directrix is y = 6 then directrix y = k p , so here 4p is distiributed for (x h) Here the equation is vertical parabola standard form(x h) 2 = 4p(y k) answered by david ExpertShow Answer The answer isIt is the equation of the horizontal or vertical line through the vertex and the center of the parabola (ie if the vertex is (3, 2) and the parabola opens up, the equation for the axis of symmetry is x = 3) 6

Today In Precalculus Go Over Homework Notes Parabolas With Vertex Other Than 0 0 Homework Ppt Download

How To Write The Equation Of A Parabola In Standard Form Video Lesson Transcript Study Com

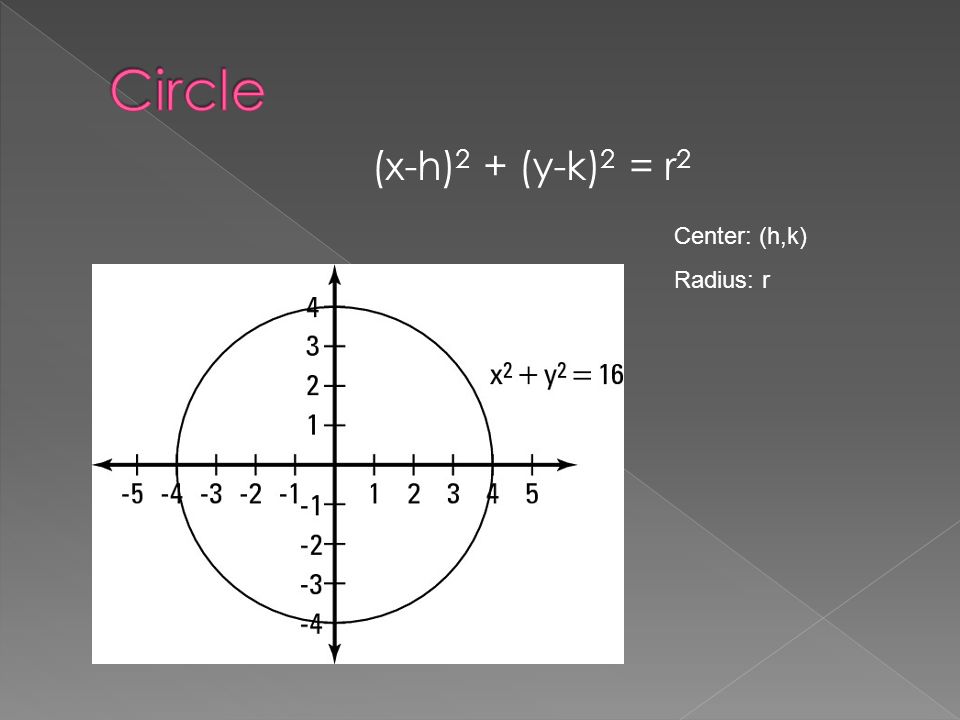
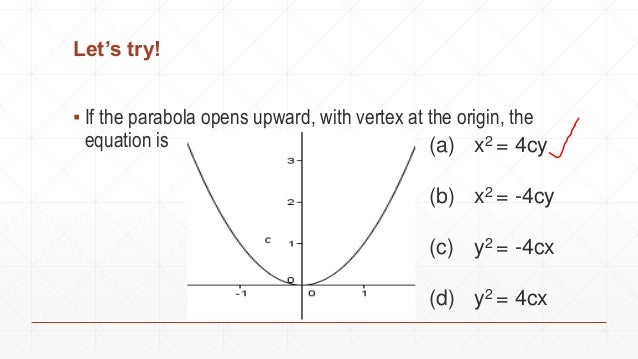
Latex{\left(xh\right)}^{2}=4p\left(yk\right)/latex Key Concepts A parabola is the set of all points latex\left(x,y\right)/latex in a plane that are the same distance from a fixed line, called the directrix, and a fixed point (the focus) not on the directrixStandard forms for parabolas x^2=4py and y^2=4px, with vertices at (0,0) or (xh)^2=4p (yk) and (yk)^2=4p (xh), with vertices at (h,k) The first equation is a parabola that open upwards The second equation is a parabola that open sideways To find p algebraically, just set the coefficient of the x or y term=4p, then solve for pSometimes you may need to complete the square first to putY = a (x h) 2 k The vertex of of the parabola is ( , ) The axis of symmetry is adirection of opening and vertical stretch or compression h horizontal translation k vertical translation

2

Conics Circles Parabolas Ellipses And Hyperbolas Math Hints

Find the yintercept Show Answer The yintercept is Use completing the square to rewrite the equation in standard form Show Answer The equation is The graph of contains the points and What is the value of a? Vertex (2,2) Focus (2,0) Directrix y=4 For future reference Formula for a parabola facing down yk=1/(4p)(xh)^2 (This is the exact same as y=1/(4p)(xh)^2k k is just on the other side) The vertex can be found by looking at our equation The vertex is (h,k) The vertex is (2,2) y2=1/8(x(2))^2 h=2, k=2 To find our focus and directrix, we need to know pAnswer Standard vertex form of vertical parabola is, (X h)^2 = 4p(Y K) Let's convert this equation in that form (3X 2)^2 = 84Y 112 => 9X^2 12X 4

Parabolas Andymath Com

More Conic Sections Objective Given A Translation I Can Graph An Equation For A Conic Section Ppt Download

The parabola in the figure has a vertical axis however it is possible for a parabola to have a horizontal axis The standard equation of a parabola is STANDARD EQUATION OF A PARABOLA Let the vertex be (h, k) and p be the distance between the vertex and the focus and p ≠ 0 ( x − h) 2 = 4 p ( y − k) vertical axis;For Exercise, an equation of a parabola (x − h)2 = 4p( y − k) or ( y − k)2 = 4p(x − h) is given a Identify the vertex, value of p, focus, and focal diameter of the parabola b Identify the endpoints of the latus rectum c Graph the parabola(yk) 2 =4p(xh) If we take the equation ( x h) 2 =4p( y k) and expand it we get x 2 2h x h 2 =4p y 4pk or x 2 2h x 4p y 4pkh 2 =0 which is an equation of the form x 2 A x B y C=0, where A, B and C are constants

1

Banner Search For Algebra Arithmetic Calculus Matrices Precalculus Probability Geometry Sets Set Theory Statistics Trigonometry Vectors Multiplication Charts Home Parabola Properties Components And Graph Parabola Properties Components

Parabola The Conic Section WorksheetFind the vertex, focus, directrix, xintercept (if any), yintercept (if any) from the general equation of the parabola Write equation in standard form(x h)^2 = 4p(y k)(y k)^2 = 4p(x h)1 Includes worksheet (compatible with Easel Activity)2 AnsweAnswer and Explanation 1 If the given equation is (x−h)2 = 4p(y−k) ( x − h) 2 = 4 p ( y − k) , then the parabola has a vertical axis The equation can be rewritten as 1 4p(x−h)2 =(y If a parabola has a vertical axis, the standard form of the equation of the parabola is this (x – h)2 = 4p (y – k), where p≠ 0 The vertex of this parabola is at (h, k)

Parabola Conic Sections

2

 If a parabola has a vertical axis, the standard form of the equation of the parabola is this (x h)2 = 4p(y k), where p≠ 0 The vertex of this parabola is at (h, k) The focus is at (h, k p) The directrix is the line y = k pF = (h,k p) and the equation of the parabola is y = 1/4p (x h) 2 k Note that vertex will always be half way between the focus and the directrix Example Find the equation of the parabola with Focus at (1,2) and directrix y = 4 Solution

Parabolas Algebra I En Equation Focus Math Parabolas Vertex Glogster Edu Interactive Multimedia Posters

Parabolas With Vertex At H K Ck 12 Foundation

Solved For The Equation Of The Parabola Given In The Form Chegg Com

2

Conic Sections Brilliant Math Science Wiki

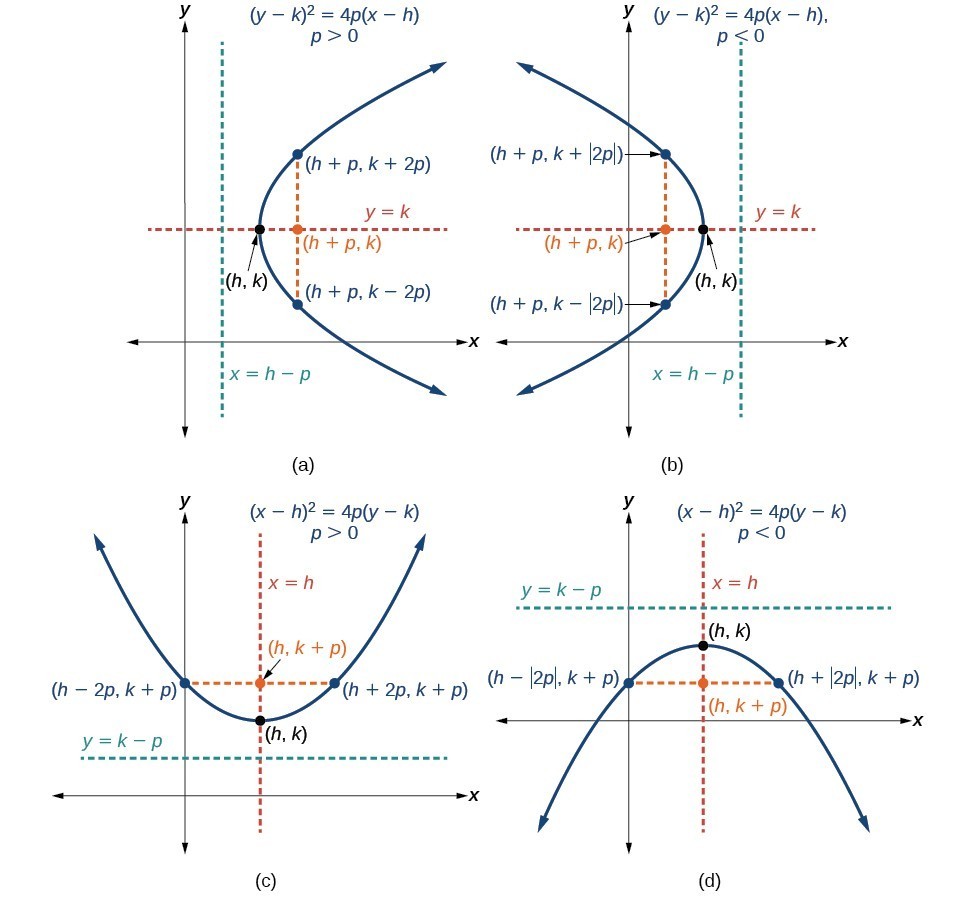
Parabolas With Vertices Not At The Origin College Algebra

Conic Section Parabola 4p Form Geogebra

Parabolas Parabolas

The Center Of The Circle Is The Vertex Of The Parabola Y 24x 12y 132 0 If The The Circle Intersects The Parabolas Directrix At A Point Where Y 11 What Would Be The Equation Of The

Chapter 11 Conic Sections Flashcards Quizlet

2

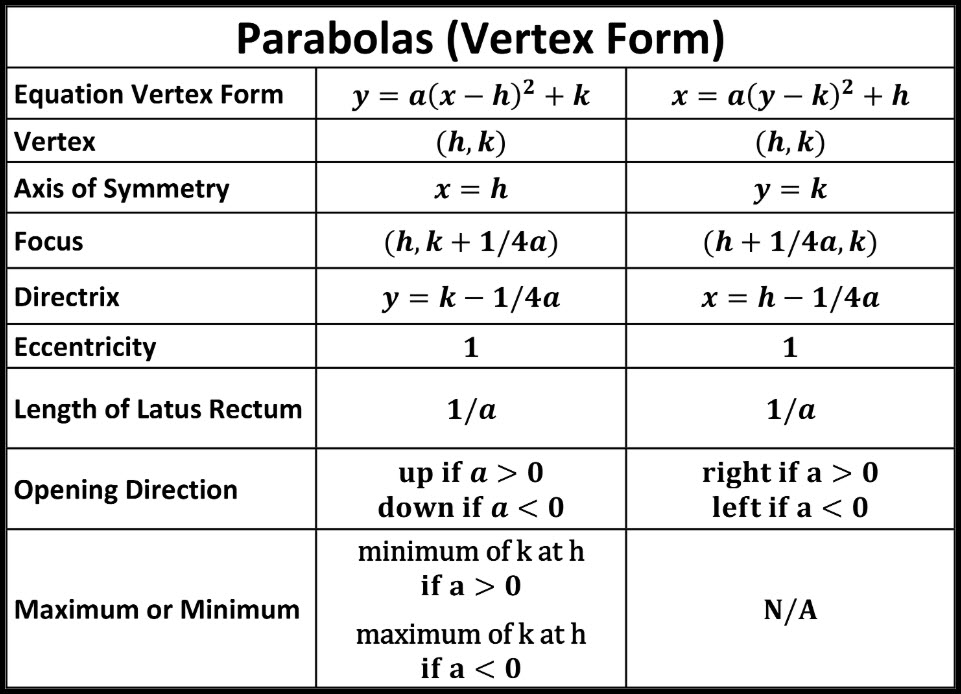
Parabolas Andymath Com

Parabolas Andymath Com

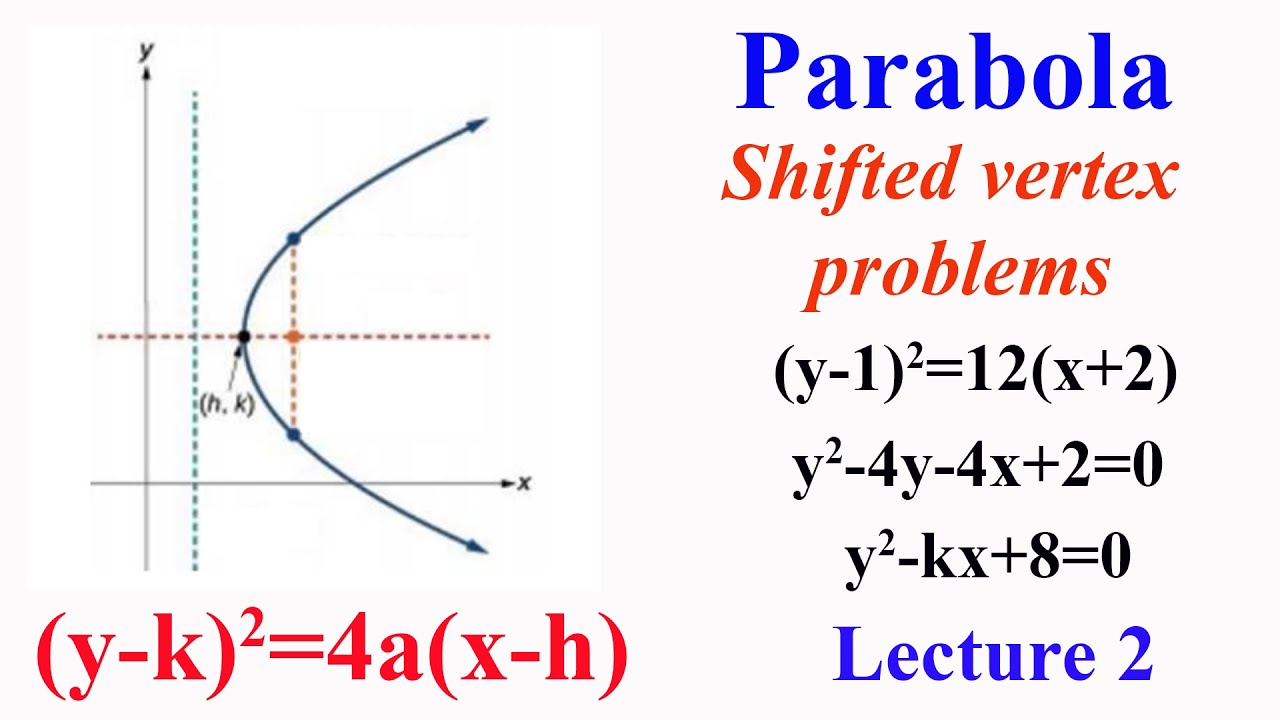
Parabola Lecture 2 Shifted Vertex Y K 2 4a X H With Examples Youtube

Solution Find The Standard Equation With Focus 2 0 And Directrix X 4 Y K 2 4p X H This Is As Far As I Have Gotten I Think That The Vertex Is 1 0

Solved 12 X 3 Y 2 2 A What Is The Axis Of Symmetry Of The Parabola Explain How To Determine This From The Equation 1 Point B What Is Course Hero

2

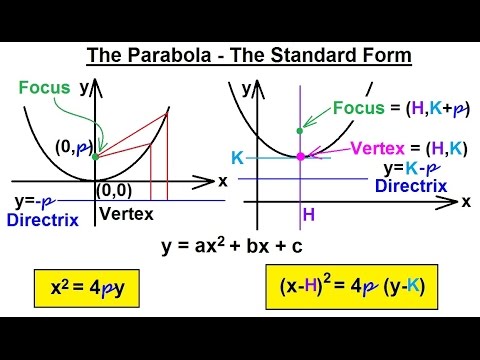
Precalculus Algebra Review Conic Sections 5 Of 27 The Parabola Standard Form Youtube

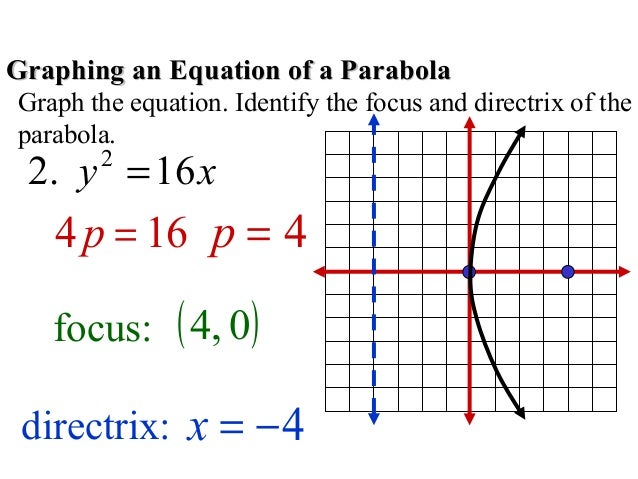
Parabola Complete

What Are The Formula Of Parabola Brainly Ph

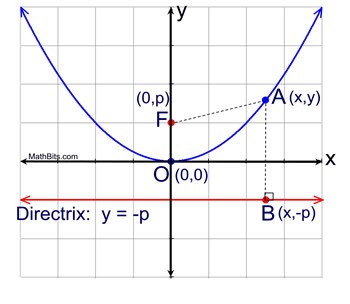
Parabola Equations Mathbitsnotebook Geo Ccss Math

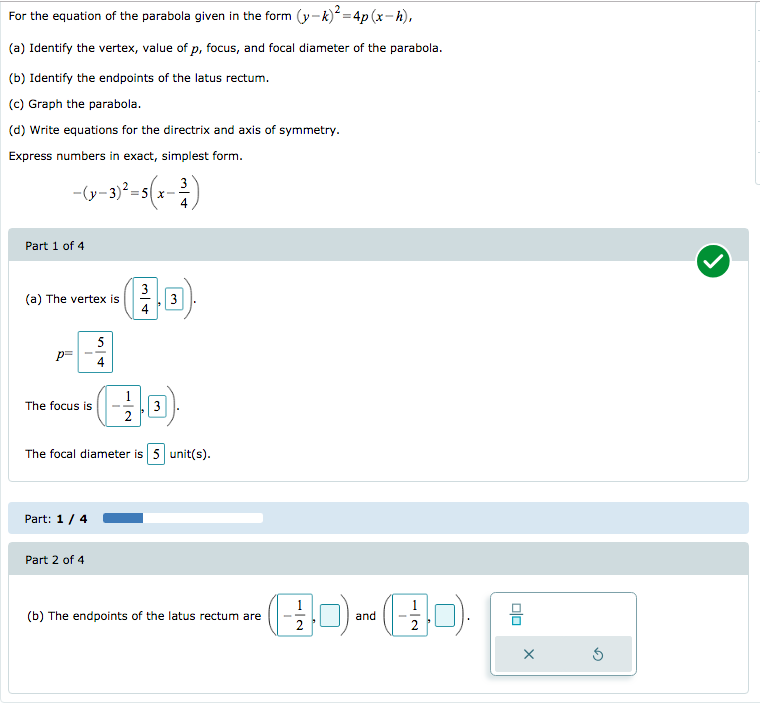
Solved For The Equation Of The Parabola Given In The Form Y Chegg Com

Precalculus Algebra Review Conic Sections 5 Of 27 The Parabola Standard Form Youtube

Conics Circles Parabolas Ellipses And Hyperbolas She Loves Math Studying Math Parabola Love Math

Parabolas

1

Conic Sections Parabolas Summary Analysis Sparknotes

Parabolas

2

Solution Focus At 2 4 Directrix The Line X 4 Find The Equation Of The Parabola Described And Two Point That Define The Latus Rectum

2

1

X H 2 4p Y K Y K 2 4p X H If The X Value Is Greater Than 1 The Parabola Will Open Up If The X Value Is Less Than 1 The Parabola Will Open Ppt Download

What Is The Equation Of The Hyperbola One Branch Of Which Has Focus And Vertex That Are The Same As Those Of X 6x 8y 23 And Whose Conjugate Axis Is On The Directrix Of

Lesson 4 Parabolas In This Lesson Students Will Become Familiar With The Equations And Graphs Of Parabolas The Definition Of A Parabola Will Be Learned Both Algebraically And Using The Distance Relationship Students Will Learn How To Construct A Parabola

10 6 Graphing And Classifying Conics Page 1 Of 2 1 1 X Y Because The Parabola Opens To The Left Pdf Document

Cbsd Org

Parabola Conic Section Warmup Graph The Following Parabola

Chapter Solutions

Solved A Write The Equation Of The Parabola In Standard Form X H 2 4p Y K And Find The Vertex By Completing The Square 3x2 6x 6y 9 B Graph And Label The Center And Four Points X 1 2 Over 9 Y 1 2

9d Zbuhbccvsrm

Unit 2 Algebra 2 With Mikhail

Parabolas

Parabolas

Solved Write The Parabola Below In One Of The Standard Forms Chegg Com

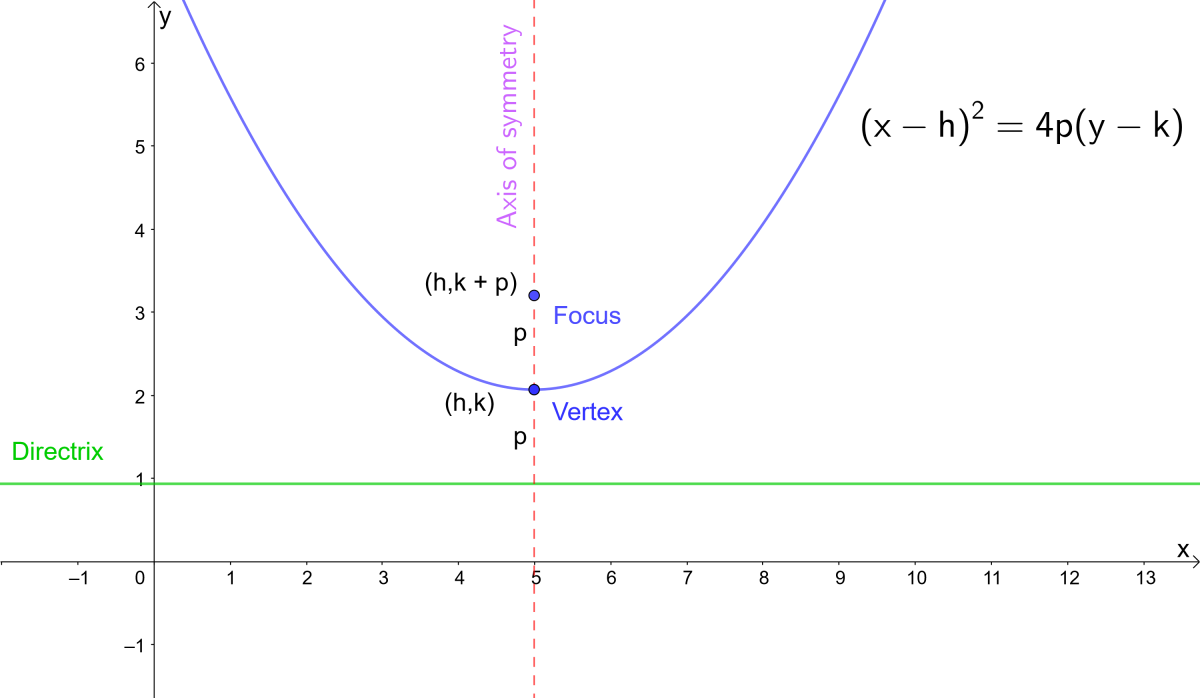
Parabola Equations And Graphs Directrix And Focus And How To Find Roots Of Quadratic Equations Owlcation

Ppt Parabola Powerpoint Presentation Free Download Id

X H 2 4p Y K Y K 2 4p X H If The X Value Is Greater Than 1 The Parabola Will Open Up If The X Value Is Less Than 1 The Parabola Will Open Ppt Download

1

Conic Sections Calculus Volume 2

Copyright C Cengage Learning All Rights Reserved Ppt Video Online Download

Parabola Equations And Graphs Directrix And Focus And How To Find Roots Of Quadratic Equations Owlcation

Properties Of Parabola

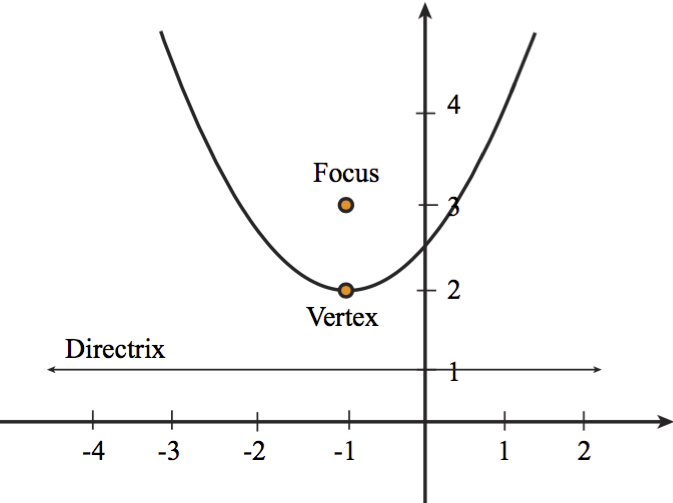
Conic Sections Conic Form Of A Parabola

Pslv Conic Section

Lesson 5 1 Parabolas Chart Parabolas With Vertex H K Vertical H K Horizontal H K X H 2 4p Y K Y K 2 4p X H 1 X H 2 4 Opens Upward If P 0 P Course Hero

Equation Of Parabola Directrix Focus Axis Problems With Solutions

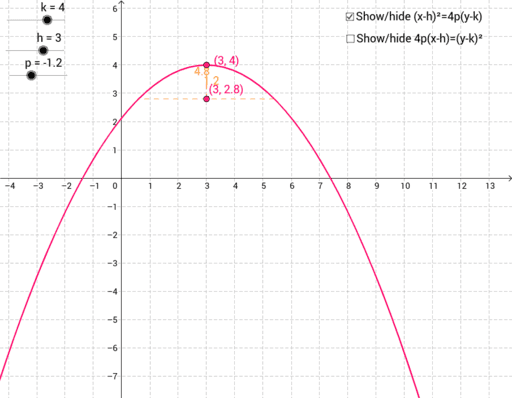
Access Parabola Equation Geogebra

Parabolas With Vertex At H K Ck 12 Foundation

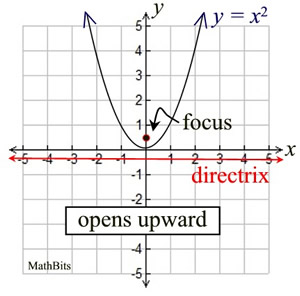
Parabola Equations Mathbitsnotebook Geo Ccss Math

2

Focus Directrix Of A Parabola From Equation Video Khan Academy

Chapter 10 Analytic Geometry Section 10 1 Parabolas Flip Ebook Pages 1 9 Anyflip Anyflip

Equation Of Parabola Directrix Focus Axis Problems With Solutions

Parabola Transporte En El Peru

Conic Sections Parabolas Summary Analysis Sparknotes

Introduction To Conics Parabolas

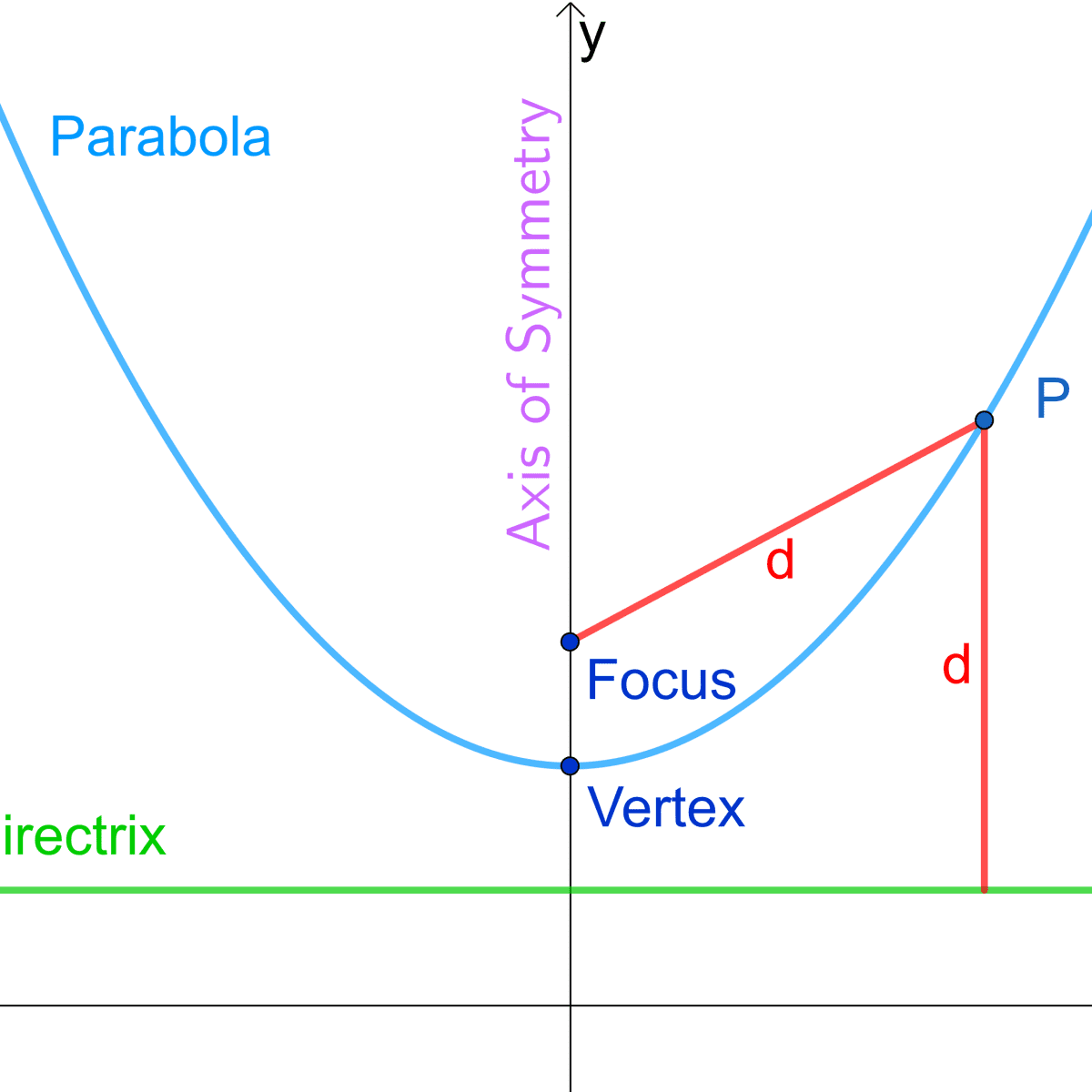
Parabola Equations And Graphs Directrix And Focus And How To Find Roots Of Quadratic Equations Owlcation

Cochranmath Copy Of Parabola

2

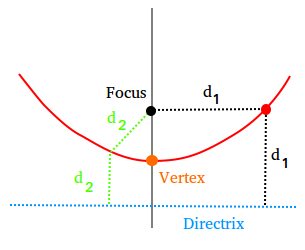
Parabola Definition And Equation

To Graph A Parabola We Need To Know The Coordinates Of Its Vertex Focus And The Equation Of Its Axis

Parabola Focus Directrix Review Article Khan Academy

Ppt 8 2 Graph And Write Equations Of Parabolas Powerpoint Presentation Id

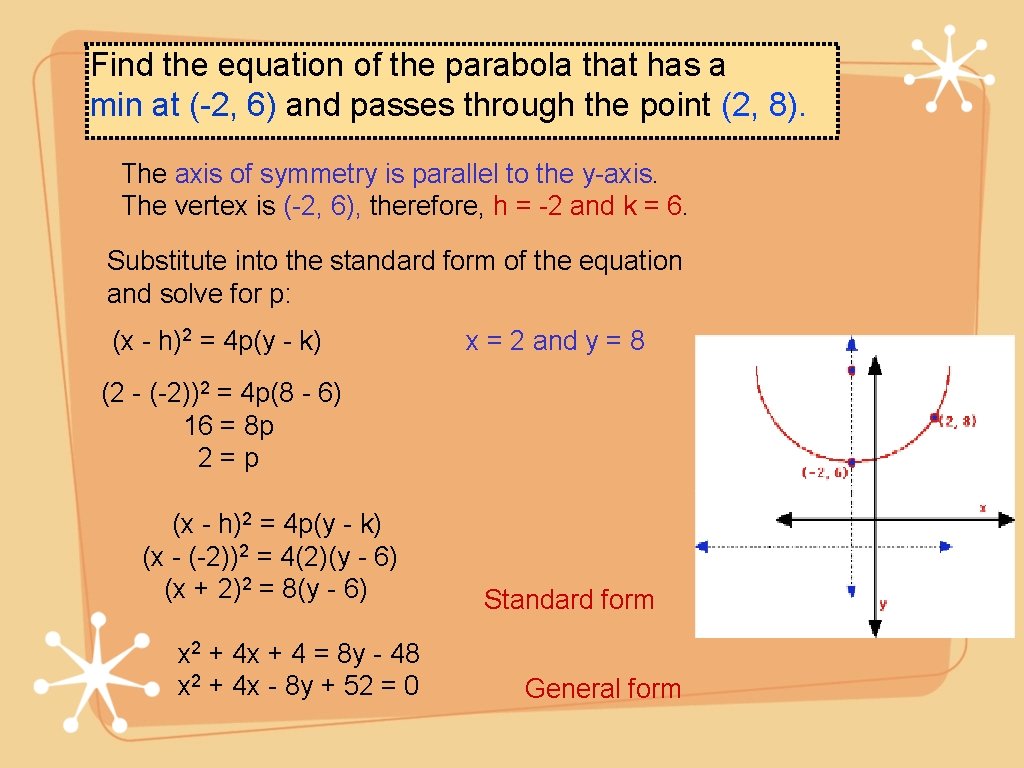
Parabola Conic Section Warmup Graph The Following Parabola

Parabola Conic Section Warmup Graph The Following Parabola

Parabolas Con Vertice En H K Ck 12 Foundation

Student Hpc Cu 10 11 8 1 Parabolas By Math Hammy Tpt

Incoming Term: parabola (y-k)^2=4p(x-h), if the focus of the parabola (y-k)^2=4(x-h), what is 4p in parabola,